[ML筆記] Ensemble - Bagging, Boosting & Stacking
ML Lecture 27: Ensemble
本篇為台大電機系李宏毅老師 Machine Learning (2016) 課程筆記
上課影片:
https://www.youtube.com/watch?v=tH9FH1DH5n0
課程網 (投影片出處):
http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML16.html















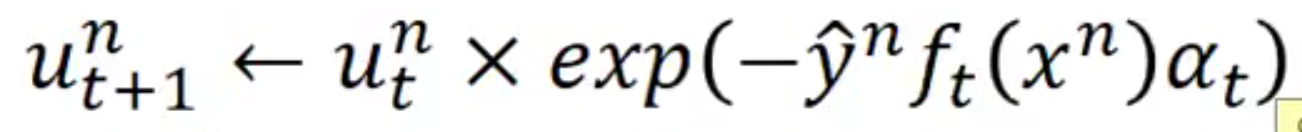








本篇為台大電機系李宏毅老師 Machine Learning (2016) 課程筆記
上課影片:
https://www.youtube.com/watch?v=tH9FH1DH5n0
課程網 (投影片出處):
http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML16.html
Ensemble 方法其實就是 “團隊合作” 好幾個模型一起上的方法
假如我們手上有一堆 Classifier ,這些 Classifier 每個都有不同的屬性,
要把他們集合起來一起合作,集合再一起需要用比較好的方法
以下來介紹一些 Ensemble 的方法
Bagging
注意:bagging 跟 boosting 使用場合不一樣
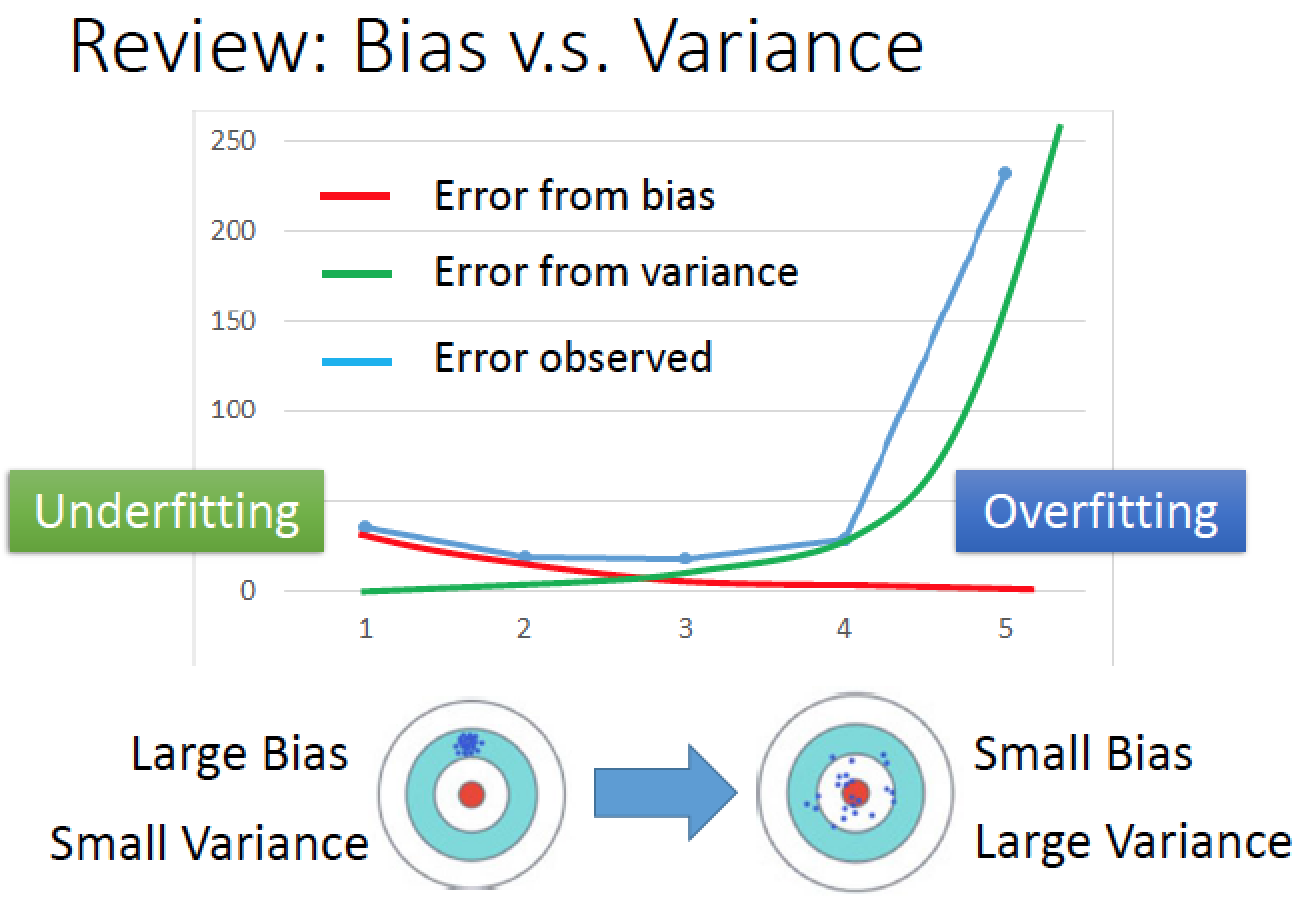
先回想一下,之前在講 Regression 時,Bias 跟 Variance 是有 trade-off
比較簡單的 model 會有 Bias 比較大,Variance 就比較小,
比較複雜的 model 會有 Bias 小 Variance 就比較大
兩者的組合下,error rate 隨著 model 複雜度增加逐漸下降,然後再逐漸上升 ( 因為 overfitting ),
忘記的話可以複習這篇:https://violin-tao.blogspot.tw/2017/07/ml-regression-part-2-where-does-error.html
忘記的話可以複習這篇:https://violin-tao.blogspot.tw/2017/07/ml-regression-part-2-where-does-error.html
之前的例子提過,在不同的世界裡面抓寶可夢,都會分別得到不同的模型,
如果不同世界裡面都用很複雜的模型,variance很大,bias 小
如果不同世界裡面都用很複雜的模型,variance很大,bias 小
把不同模型的輸出,通通集合起來,做一個平均,得到一個新的模型 f-hat 可能就會跟正確的模型很接近,
Bagging 就是要體現這件的事情!
Bagging 就是要體現這件的事情!
Bagging 做的事情就是:
雖然我們不可能到不同的宇宙去蒐集 data ,但是我們可以自己創造出不同的 dataset
再用不同 dataset 各自去 training 出複雜的 model 雖然
隨然每一個複雜的 model 獨自拿出來看 variance 都很大,
但是把不同的 variance 很大的 model 集合起來以後,他的 variance 就不會這麼大,且他的 bias 會是小的!
但是把不同的 variance 很大的 model 集合起來以後,他的 variance 就不會這麼大,且他的 bias 會是小的!
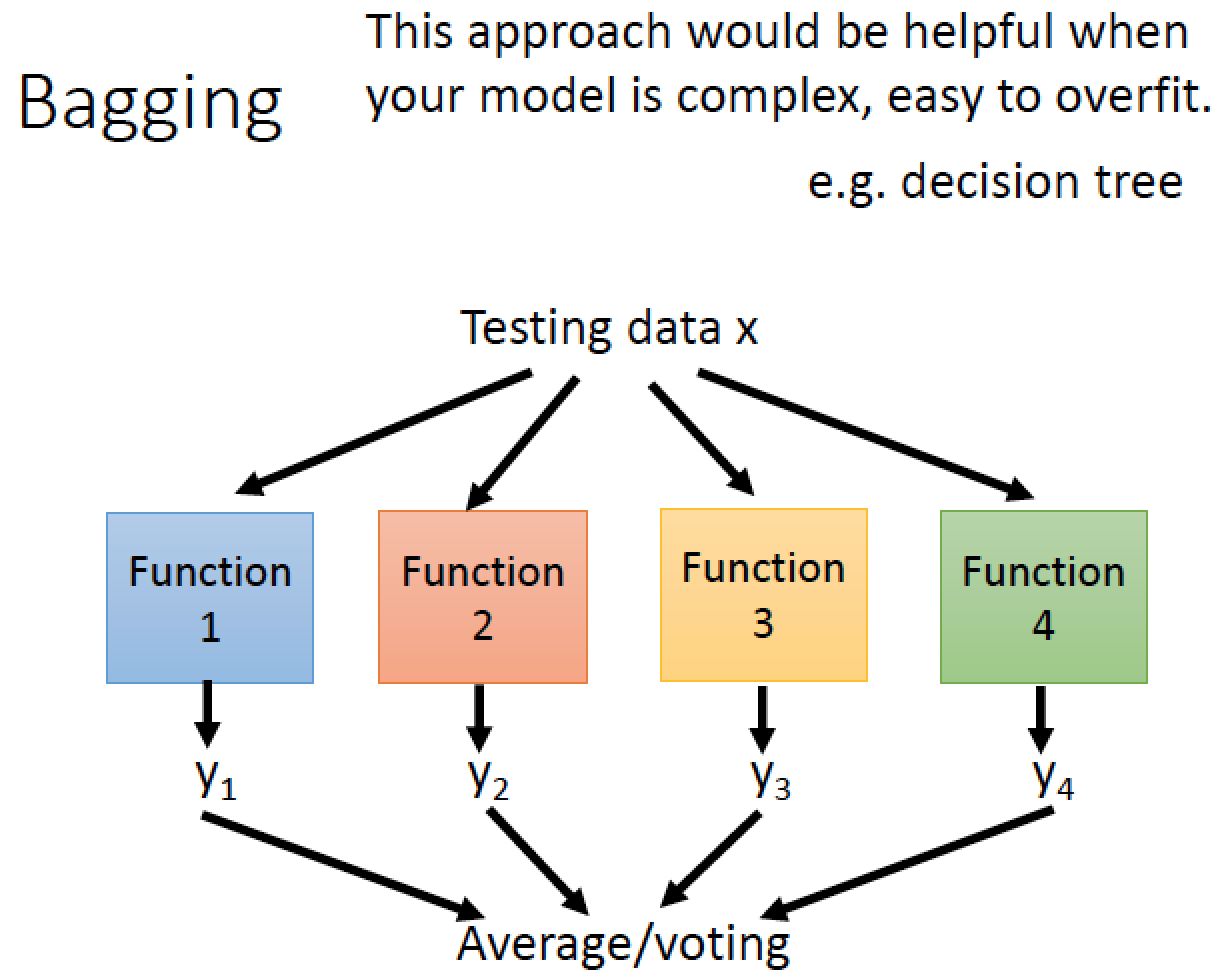
從 N 筆 training data 中,做 sampling 組成 M 個 dataset 每個 dataset 裡面有 N’ 筆資料
使用 sampling 的方法建出很多資料集,訓練出多個 function
接著再把我們訓練出來的四個 function 跑出來得結果,拿出來整合,得到最後的結論
如果是 regression 問題,就把 functions output 做平均
如果是 classification 問題,就做 voting
decision tree 是一個非常容易 overfitting 的方法,只要 tree 夠深,
一定能夠在 training data 上面做到 100% 的正確率,但是不見得能夠再 testing 時表現得好
一定能夠在 training data 上面做到 100% 的正確率,但是不見得能夠再 testing 時表現得好
所以我們使用的 model 容易 overfitting 時,就需要做 bagging,decision tree 就是一個例子!
輸入的 x1 < 0.5 就是 Yes 否則是 No,x1 yes 的條件下 x2 < 0.3 就是 Yes 否則是 No
我們把最後的 Class1 塗藍色,Class2 塗成紅色,即可得到結果圖
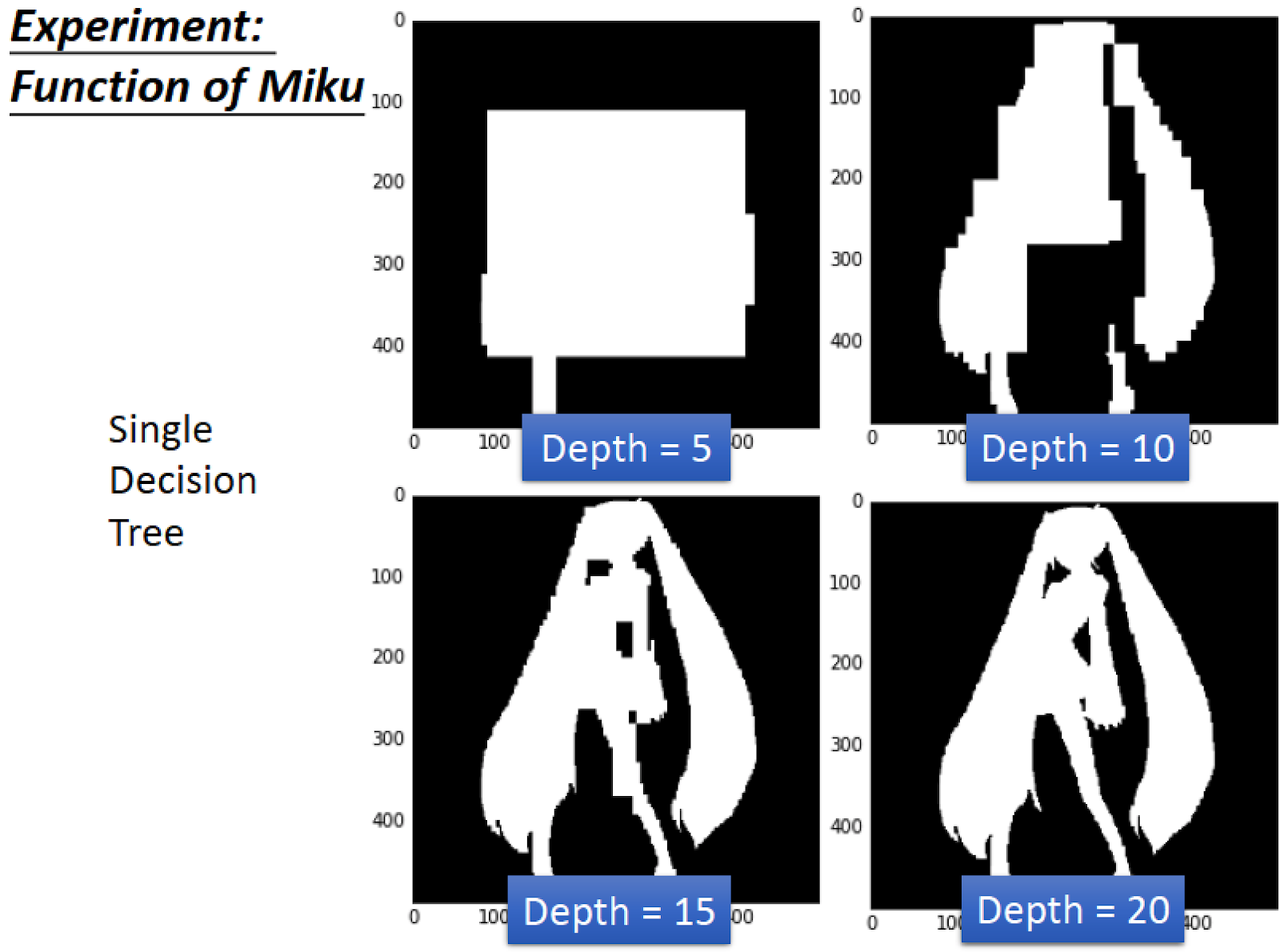
舉一個實際的例子
當 Decision Tree 深度只有 5 的時候,完全看不出來
如果淺淺加深深度,到 20 的時候,可以成功地把初音描繪出來
Decision Tree 只要樹夠深,可以做出任何 Function
對 Decision Tree 做 Bagging 就是 Random Forest
Random Forest
使用傳統 Bagging 的方法可以做 Random forest 但是得到的 Tree 每一科都沒差太多。
Random Forest 比較常見的做法是
在每一次要產生 brench 的時候,都 random 決定,哪一些 feature 或哪些 question 是不能用
這樣的機制下,可以使得就算使用一模一樣的 dataset ,
我們每一次產生的 Decision Tree 都是不一樣的
我們每一次產生的 Decision Tree 都是不一樣的
一般在做 train 時會把手上的 label data 切成 training set 跟 validation set
但使用 bagging 的時候,可以不用把 data 切成 training set 跟 validation set
同樣可以擁有 validation 的效果 → 這樣做 Out-of-bag validation:
同樣可以擁有 validation 的效果 → 這樣做 Out-of-bag validation:
做 bagging 的時候,訓練出來的 function 都是用部分的 data train 出來的:
f1 只用 x1,x2 train
f2 只用 x3,x4 train
f3 只用 x1,x3 train
f4 只用 x2,x4 train
所以
可以用 f2 跟 f4 bagging 的結果在 x1 資料集上去測試
可以用 f2 跟 f3 bagging 的結果在 x2 資料集上去測試
可以用 f1 跟 f4 bagging 的結果在 x3 資料集上去測試
可以用 f1 跟 f3 bagging 的結果在 x4 資料集上去測試
接下來把 x1 ~ x4 的所有測試結果把它平均計算 error rate,得到 out-of-bag (OOB) error
這個結果可以反應測試的正確率
接下來,看一下 random forest 在做初音的實驗的結果
如果做 100 棵樹,觀察深度變化的結果
我們可以看到深度 = 10 的時候,比較平滑了
深度 = 15 時,也比之前的結果平滑
Boosting
剛剛的 bagging 是用在很強的 model
boosting 則是用在弱的 model
Bossting 的保證:假設你有一個 Model 錯誤率高過 50% 只要能夠做到這件事情,
boosting 可以把這些錯誤率值略高於 50% 的Model 降到 0%
boosting 可以把這些錯誤率值略高於 50% 的Model 降到 0%
核心想法:我們找很多個 classifier f1,f2,f3, … 如果找到 f2 跟 f1 是互補的,
f2 要去做 f1 無法做到的事情,然後再找到 f3 也要跟 f2 互補,這樣一直找一大把後集合起來,就會很強
f2 要去做 f1 無法做到的事情,然後再找到 f3 也要跟 f2 互補,這樣一直找一大把後集合起來,就會很強
使用 Boosting 在找 f1, f2, f3 的過程中,是要有順序的,
因為每次找的人都要能夠做到上一個人沒辦法辦到的事情!
因為每次找的人都要能夠做到上一個人沒辦法辦到的事情!
那麼,怎麼得到不同的 Classifier ?
可以製造不同的 traing set 來做到 by re-sampling
也可以透過 re-weight 來做:
假如我們有三筆 data 每一筆 data weight 都給予不一樣的權重,
在 training 的時候 loss function 在計算每一筆 error 的時候在前面乘以該筆 data 權重值,
使得他在 training 的時候被多考慮一點,或是被多忽略一點!
Boosting 有很多種,其中一種經典的事 Adaboost
Adaboost 的想法:
要找一組新的 training data 使得讓 f1 在新的 data 上面結果會爛掉,正確率會接近 50%
然後再用這組新的 training data 上面來訓練 f2
然後再用這組新的 training data 上面來訓練 f2
如何找新的 training data 可讓 f1 壞掉呢?
定義 eslon_1 為 f1 再 training data 上的 error rate
其中 eslon_1 會 < 0.5,我們不可能讓 error 超過 0.5,
因為 error rate 大於 0.5 時只要把結果相反來看就好了)
因為 error rate 大於 0.5 時只要把結果相反來看就好了)
假設原來的 training data weight 是 u1
新的 training data weight 是 u2
我們目標是把 u1 換成 u2 ,讓 f1 的 error rate epsilon_1 = 0.5,
使得 f1 的表現看起來就像是隨機的一樣。
得到 u2 後,拿 u2 作為 weight data 然後拿這樣的 dataset 去訓練 f2,
這樣訓練出來的 f2 就會補足 f1 的弱點!
舉例說明:
如圖,我們假設有四筆 training data,f1 目前答對三個,答錯一個 error rate = 0.25
接著我們要改變 data 的權重,讓 f1 答對的 data 權重變小,答錯的權重增加,
讓 f1 表現出來的 “得分” 變得很糟糕 (error 變大)
讓 f1 表現出來的 “得分” 變得很糟糕 (error 變大)
調整後的 error rate = sqrt(3) / (2 * sqrt(3)) = 0.5
分母:3 * ( 1 / sqrt(3) )+ sqrt(3) = 2*sqrt(3)
分子:sqrt(3)
然後我們再這組新的 “配分” 的 data 上去訓練 f2
如果 xn 被 f1 分類錯誤,那我們就把 xn 乘上一個權重 d1 其中 d1 > 1
如果 xn 被 f1 分類正確,那我們就把 xn 除上一個權重 d1 , d1 > 1
那麼
d1 的值要設多少呢? 才能使得 f1 的 error rate = 0.5
結論 d1 = sqrt((1-epsilon1)/epsilon1)
AdaBoost 演算法
training data 一開始初始的 weight 都是 1
接著跑 T 次 iteration
每一筆 data 都有一個 weight 值 u
每一次的 iteration 會計算出一個 epsilon_t 然後根據 epsilon_t 的值來更新 weight
因為 dt = sqrt( (1 - epsilon_t ) / epsilon_t )
另一種表示法,定義 alpha_t = ln( dt ) = ln( sqrt( (1 - epsilon_t ) / epsilon_t ) )
有了 alpha_t 就可以把式子變得更簡便一點:
Uniform weight:
把 T 個 Classifier 值通通加起來再取正負號,整合起來看結果
Non-uniform weight:
但是 T 個 Classifiers 當中的表現有好有壞,所以在每一個 classifier 的結果前面
再乘以一個權重 alpha_t 這樣下去整合結果會更好
再乘以一個權重 alpha_t 這樣下去整合結果會更好
alpha_t 的精神:
如果某個 classifier 錯誤率 epsilon_t = 0.1 可以計算出 alpha_t = 1.10
如果另一個 classifier 錯誤率 epsilon_t = 0.4 計算出來的 alpha_t = 0.20
所以 classifier 的錯誤率越小,分辨的比較準的時候 alpha_t 就會比較大!
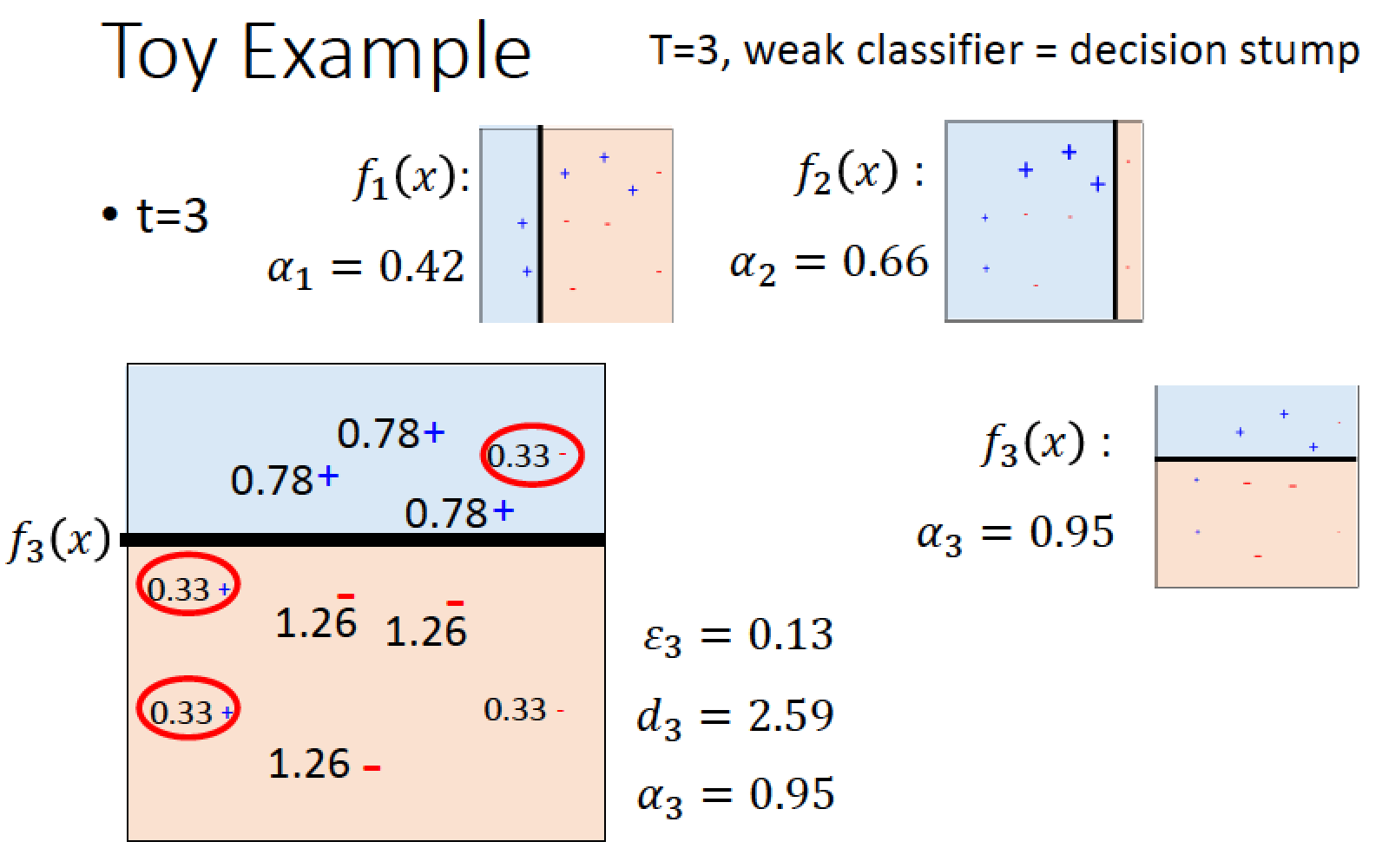
舉個實際的例子:
平面上有 10 筆資料,要做二元分類
f1 分類器切下去,發現有 3 筆分類錯誤,所以錯誤率 epsilon_1 = 0.3
並可以由 epsilon 的值計算出 d1 = 1.53, alpha_1 = 0.42
接著,我們把分類錯的資料 weight 變大乘以 1.53 (d1),分類對的 weight 變小 除以 1.53 (d1)
然後我們使用新的 classifier f2 切一刀,左邊是 positive 右邊是 negative,
針對我們上一步驟調整後的 data 來做分類
針對我們上一步驟調整後的 data 來做分類
f2 總共分類錯三筆 data,經過計算,可以得到 f2 的 error rate: epsilon_2 =
(0.65 * 3) / (1.53 * 3 + 0.65 * 7) = 0.21
再根據 epsilon_2 可以計算出 d2 = 1.94, alpha_2 = 0.66
然後我們把分類錯的資料 weight 變大乘以 1.94 (d2),分類對的 weight 變小除以 1.94 (d2)
更新 data weight
第三個 classifier 切一刀,上面是 positive 下面是 negative,總共分錯三筆資料
根據前面的方法,再次操作一遍,得到 epsilon_3 = 0.13, d3 = 2.59, alpha_3 = 0.95
假設我們只跑三個 iteration 就結束了,所以 weight 就打住不更新了
整合起來,得到最後的 Classifier H(x)
目前三個 classifier 把空間切成六塊
左上角:大家都覺得是藍色的,沒有爭議就是藍的
右上角:f1 跟 f2 覺得是紅的 總共佔 0.42 + 0.66 = 1.08 , f3 覺得是藍的但只有 0.95 輸了,
所以結論,右上角是紅的
所以結論,右上角是紅的
左下角:f1, f2 都覺得是藍的,總共 weight 1.08 > f3 覺得是紅的且 weight 0.95 也輸了!
所以結論,左下角是藍的
f1, f2, f3這三個 classifier 分別都會犯錯,
但是我們透過 AdaBoost algorithm 把它們組合起來後,得到好的結果!
但是我們透過 AdaBoost algorithm 把它們組合起來後,得到好的結果!
證明:AdaBoost 跑的 iteration 越多, performance 越好
假設我們有 N 筆 data
| |
AdaBoost 的神祕現象:
橫軸 iteration 縱軸 error rate
我們發現 training data 的 error rate 在五個 weak classifier 合力下就會變 0 了
加了更多的 weak classifier 後,training data error 已經不會再下降,但是 testing error 居然還能持續下降
如果我們 train weak classifier 的演算法可以讓 error rate 變零的話,使用 Adaboost 是會有問題的!
Adaboost 的使用時機是,使用在一大堆 weak classifier 上,所以一定要是 weak 不能太強!
g(x) : 代表 weak classifiers 整合後的 output 我們希望 g(x) 是個非常大的值
定義:g(x)*y-hat 為 Margin 也就是使用整合後的分類器,分類正確的情形
Adaboost 的 (upper bound) Margin 變化圖,可以發現,
只有 5 個 weak classifier 時,margin 是虛線,但是增加 weak classifier 的數量時,
增加到 1000 個 classifiers 時我們發現 Margin 會增加,如圖中的黑色實線
雖然在 training set 的 error rate 已經是 0 不會再下降,
也就是 y-hat 已經跟所有的 g(x) 同號了,但是增加 classifier 數量時,
仍然可以讓 margin 增加,使得在 testing 的 error rate 下降
使用深度為 5 的 decision tree,之前的實驗中,深度 5 的 tree 幾乎都是不能用的
但是用 Adaboost 可以發揮群眾的力量
找 10 棵 tree 結果就有輪廓出來了
20 棵 tree 時結果更好了
找 100 棵 tree 時,幾乎可以把完整的初音描繪出來了!
Stacking
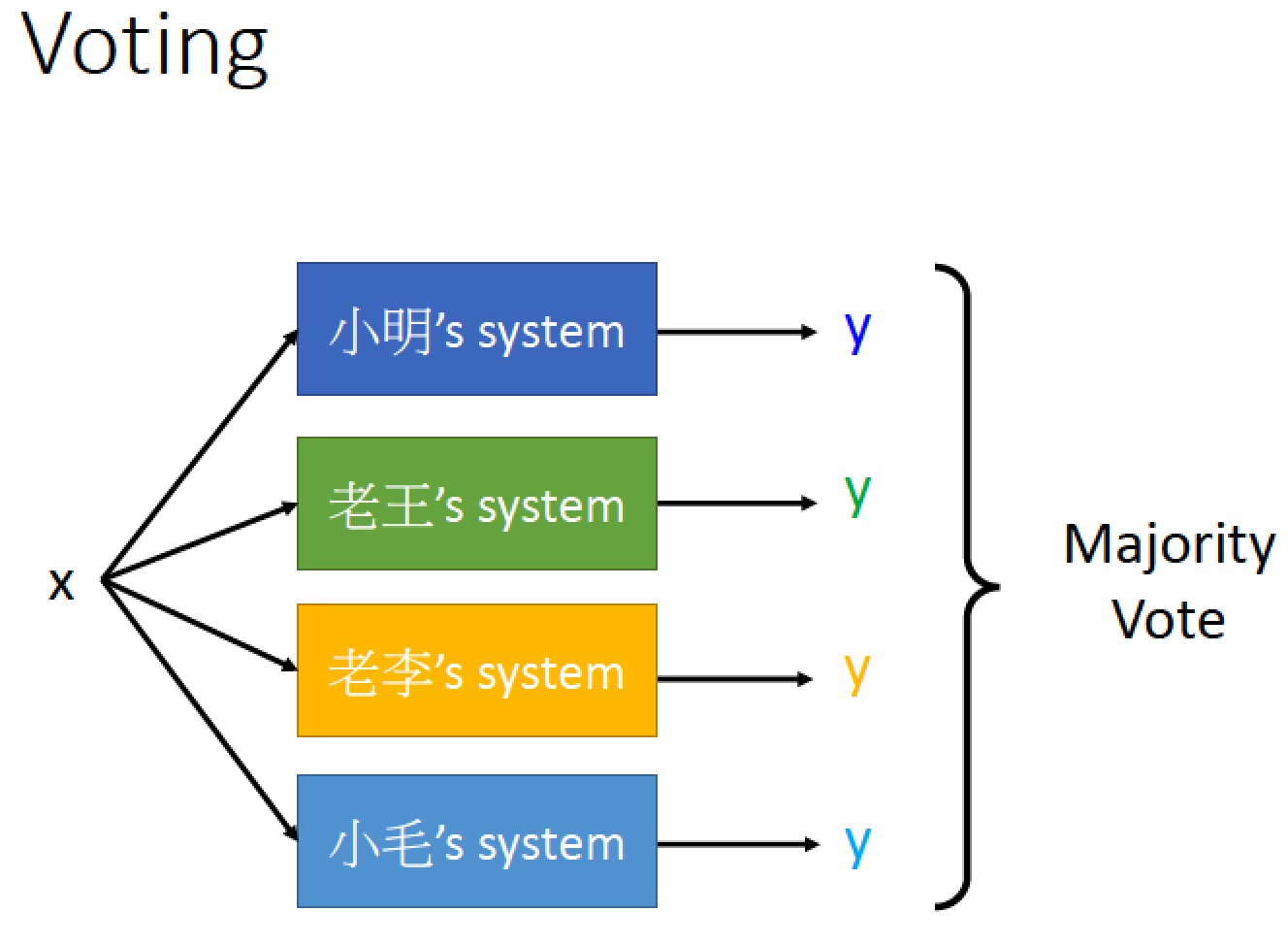
投票會遇到的問題:
並不是每一個系統都是好的,例如小明的 Classifier 根本亂寫,
但是他還是佔一票,這樣可能會把投票結果變糟
但是他還是佔一票,這樣可能會把投票結果變糟
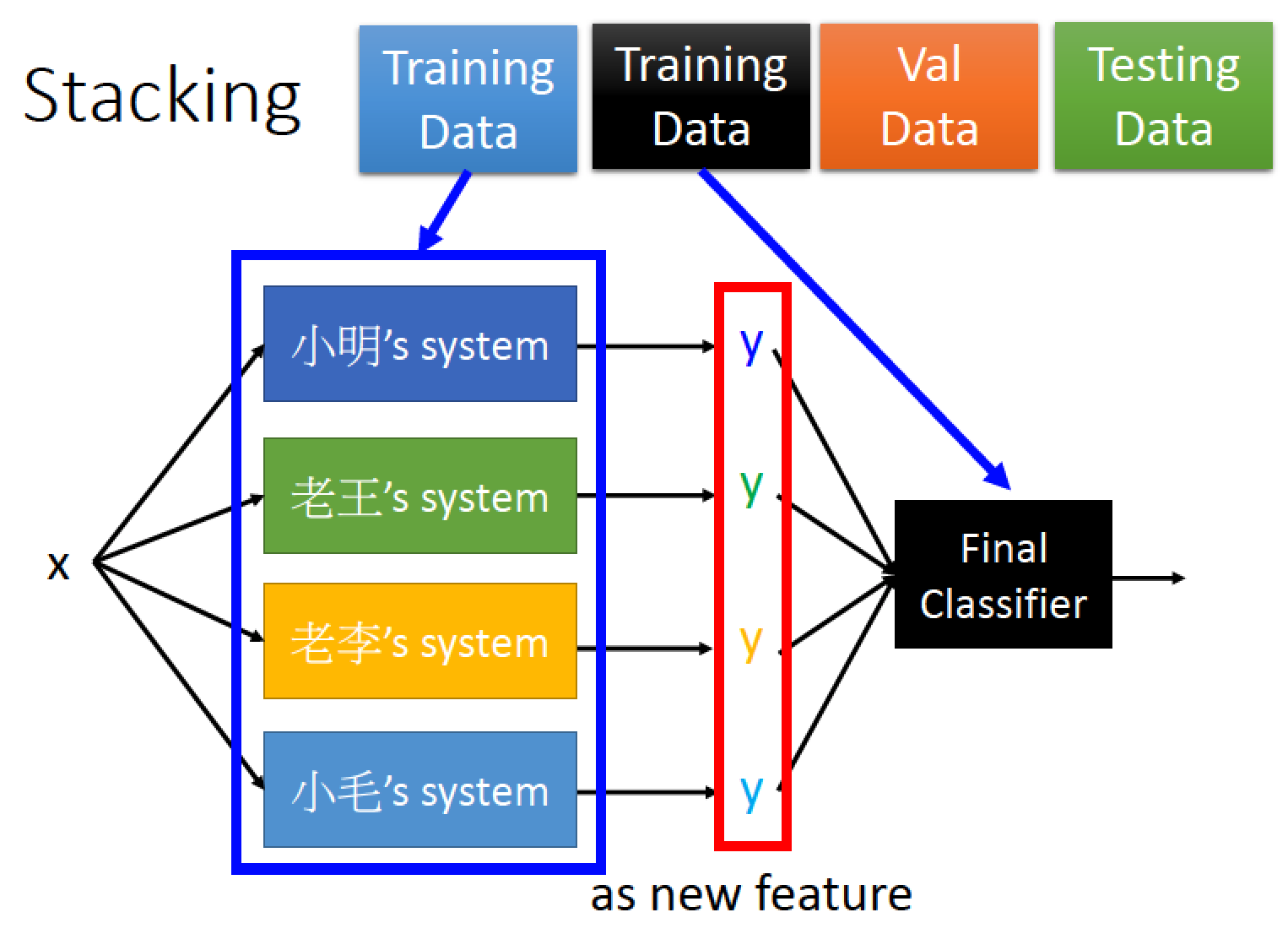
使用 Stacking 方法
把 training data 切成兩部分
一部分拿來 Learn 前面的 classifier
另一部分拿來 train 後面的 Final Classifier
Final Classifier 可以不用太複雜,倘若前面的都太複雜了,
那最後的 Final Classifier 可以是單純的 Logistic regression 就可以了
那最後的 Final Classifier 可以是單純的 Logistic regression 就可以了



留言
張貼留言