ML Lecture 25: Recurrent Neural Network (Part I)

本篇為台大電機系李宏毅老師 Machine Learning (2016) 課程筆記
上課影片：
https://www.youtube.com/watch?v=xCGidAeyS4M
課程網 (投影片出處)：
http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML16.html

首先來看一個問題：Slot Filling

我們要理解客戶講的一句話，必須把一些關鍵字詞抽取出來做分類

上述的話當中，要把關鍵字 Taipei 分類為 Destination，

Nov. 2nd 分類在 time of arraival 這個類別中

該怎麼做呢？

一個直觀的作法就是，把 Taipei 丟進一個 Network 裡面，然後最後跑出他的分類

把一個詞彙丟進 Network 當中，要先把它轉換成 feature vector

把詞彙 encode 成 vector 的方法很多，其中一種就是 1-of-N encoding

1-of-N Encoding 的方法簡單解釋

把所有會看的單字作為一個很大一串的 vector

對於每一個出現的字，都可以用 vector 當中的其中一個元素表達

例如 [apple, bag, cat, dog, elephant]

dog 出現在 vector 當中的第四個位置，所以 dog 被 encode 成 [0,0,0,1,0,]

這樣的 encode 的方法還是很難概括所有可能看到的詞彙，所以我們再加一個 other 維度，可以代表目前未收錄在 vector 當中的其他詞彙

也可以用某一個詞彙的字母來表示 vector 例如 word hashing

無論如何，我們可以把一個詞彙表示成一個 vector

再將這個 vector 丟進一個 Feedforward Network 裡面去做分類，output 出這個詞彙屬於每一個 slot 的機率

但是光只有這樣是不夠的

假設有一個使用者說 arrive Taipei … 此時 Taipei 這個詞彙要分類在 destination

另一個使用者說 leave Taipei … 這個時候，Taipei 要被分類在 place of departure

如果我們讓 Neural Netword 是有 “記憶力” 的他就可以記得之前看過 arrive 或 leave 這個字詞

這樣就可以解決 input 同一個詞彙，但是 output 必須不同的問題

這種有記憶力的 Neural Network 就是 RNN

每一次的 hidden layer 產生出的 output 都會被存起來到藍色的方塊裡面

當我們下一次有 input 進來的時，除了考慮 input 的值以外，也會考慮存之前被放在藍色方塊memory 裡面的值。

舉例：

假設我們這個 network 所有的 weight 都是 1，所有的 activation function 都是 linear

還沒放進任何東西之前，給 Memory 初始值 0 跟 0

當我們第一次輸入 [1 1] 時，hidden layer 中途的結果 [2 2] 被寫進memory 了，最後計算出來的 output 是 [4 4]

當我們下一個 input [1 1] 時

因為前一回合中間的的結果 [2 2] 被記起來了，

所以這次輸入除了考慮 [1 1] 以外，也加上了 [2 2] 總共輸入為 [3 3] 經過 hidden layer 運算後最後得到 [6 6]，又被存放到 memory 當中，本回合最後計算結果得到 [12 12]

因此我們兩次都是輸入 [1 1] 但是兩此得到的 output 的結果變得不同了！

我們下一個 input 是 [2 2] ，經由加上 memory 機制的運算後最後得到 [32 32]

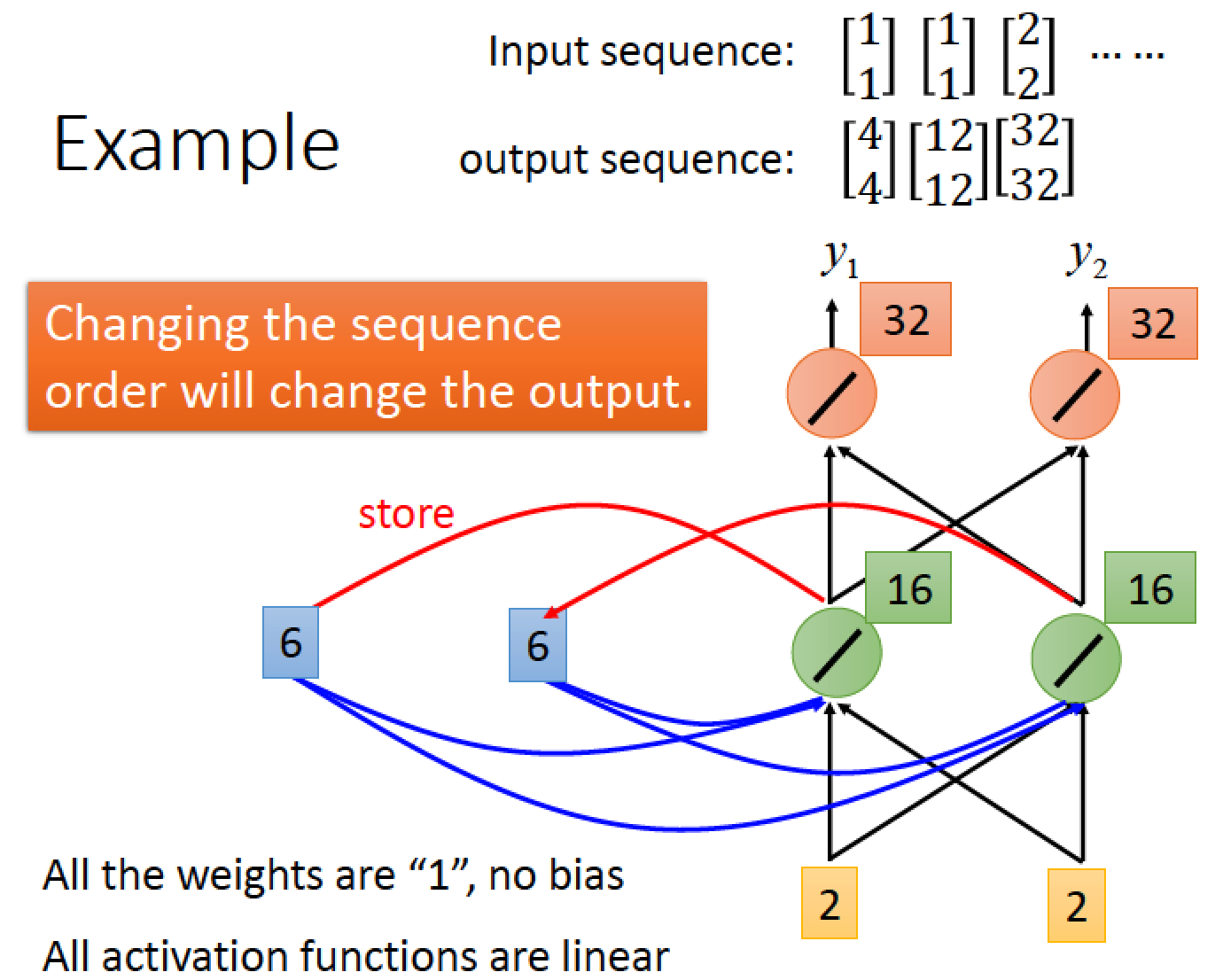
RNN 在考慮 input 的 sequence 的時候，並非是 independent

也就是 RNN 會考慮 input sequence 的 order，

所以任意調換 input 的順序，他的 output 結果是會不一樣的

hidden layer 的 output 為 a1 被存進 memory 裡面，並且會影響到下一回合的運算

上圖中，同樣的 weight 用同樣的顏色表示，看起來有三個 network，實際上是同一個 network 在三個不同的時間點被使用

這樣的機制下，我們就可以做到 “同樣的 input 但必須產生不同的 output” 這件事

例如 Taipei 前面放 arrive，當讀取到 Taipei 的時候，他會受到前一回合分析 arraive 的特性的影響，最後綜合起來判斷這回合的 Taipei 應該要被分在哪一個類別

同理，在Taipei 前面放 leave，當讀到 Taipei 時，則會受到前一回合分析 leave 的 hidden layer 的 output 影響

當然我們的 RNN 可以是 Deep 的

對於每一層 hidden layer，都可以使用 memory 機制去影響下一回合的 hidden network

RNN 的其他變型

我們前述的都是 Elman Network 每一層 hidden layer 參數都記起來傳下去

另一種是 Jordan Network 他存的是整個 network 的 output 值

據說 Jordan Network 可以得到比較好的 performance，因為它記起來的是最後的結果，學到的東西比較有目標性

而 Elman 記起來的部分是中途過程中的每一層 hidden layer 的值，中途的 hidden layer 是沒有 target 的，所以很難控制能學到的東西

RNN 也可以是雙向的

也就是我們讀取方向可以是反過來的

所以我們可以同時做 train 正向的 RNN 再同時 train 逆向的 RNN

然後分別把所有正向與逆向計算出來在時間點 t 輸入 xt 的 hidden layer 參數輸出都丟給 output layer 讓 output layer 去產生結果 yt

雙向的好處是，我們在產生 output 時，我們不止有看了從句首到句尾這個方向，同時也看了句尾到句首的方向，這樣雙向的理解比較全面

目前為止都還是 RNN 的基本簡單款，接著要看 RNN 比較複雜的內容

剛才看的 memory 都是比較單純的，可以隨時把值存進 memory，也可以隨時把值從 memory 讀出來，比較進階的 memory 策略為 LSTM

Long Short-term Memory (LSTM)

輸入的地方有一個 Input Gate，當它打開時，外界的 input 才能存進來 Memory Cell

輸出的地方也有一個 Output Gate，當它打開時，Memory Cell 裡面的值才能傳出去

另外有一個 Forget Gate，當它打開時，會把 Memory Cell 裡面的值 “忘掉”

這些 Gate 何時要打開或關掉，是要透過 Network Training 自己去學的

因此整個 LSTM 共有 4 個 input，1 個 output

4 個 input：1 個想要被存進 Memory Cell 的值跟 3 個用來操控 Gate 的訊號

我們把整個 LSTM 詳細參數攤開來看

zi：控制 input gate 的 signal

zo：控制 output gate 的 signal

zf：控制 forget gate 的 signal

z：要被存進 cell 的 input value

a：output

z 通過一個 activation function 得到 g(z)

zi 通過一個 activation function 得到 f(zi)

zo 通過一個 activation function 得到 f(zo)

zf 通過一個 activation function 得到 f(zf)

f 通常用 sigmoid function 因為 sigmoid function 值介在 0 ~ 1之間，代表 gate 被打開的程度

如果 f 的 output 是 1 代表 gate 打開，反之 output 是 0 代表 gate 被關閉

c’ 為新的存在 memory 裡面的值

c’ = f(zi)*g(z)+c*f(zf)

由上式可知，f(zi) 控制 input g(z) 是否可以進來，因為當 f(zi) = 0 時，前面那一項就是 0

而 f(zf) = 1 時，代表之前的 c 會被記得，跟這回合的 input 值相加

f(zf) = 0 時，代表之前的 c 會被遺忘，後面那一項會是 0

所以 forget gate 的特性跟字面上的直覺剛好相反

當 forget gate 打開時 f(zf) = 1，之前的值會 “記得”

當 forget gate 關閉時 f(zf) = 0，之前的值會 “遺忘”

用個 LSTM 例子實際來跑跑看：

y 是我們該回合的輸出	x1 為 input 收到的值 x2 為 forget gate x3 為 output gate
藍色框部分是 memory 裡面的值第二回合中 forget gate 是 1 所以會把 input 3 給記起來，所以第三回合的 memory 當中是 3	第四回合的 forget gate 也是 1 此回合的 input 是 4 且目前存放在 memory 裡面的值是 3 所以在第五回合 memory 裡面的值更新成 3+4 = 7 (藍色框) 第六回合的 output gate 是 1 所以會在 output y 的地方看到我們目前 memory 存放的值 7 output 值為 7 (紅色框)
第七回合的 forget 是 -1 所以 memory 裡面的值要被 reset 成 0，然後第八回合又把該回合收到的 input 6 記起來	最後的 output 得到 6